Step 1 – Work out current gearing
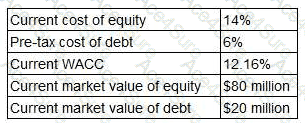
Current values:
Equity = $80m
Debt = $20m
Total value VVV = 80 + 20 = $100m
So:
DE=2080=0.25\frac{D}{E} = \frac{20}{80} = 0.25ED=8020=0.25
Tax rate T=20%T = 20\%T=20% → after-tax cost of debt:
Kd(1−T)=6%(1−0.2)=4.8%K_d(1-T) = 6\%(1-0.2) = 4.8\%Kd(1−T)=6%(1−0.2)=4.8%
Given cost of equity Ke=14%K_e = 14\%Ke=14%.
Step 2 – Find the ungeared (asset) cost of capital KuK_uKu
Use Modigliani–Miller with tax for equity:
Ke=Ku+(Ku−Kd)(1−T)DEK_e = K_u + (K_u - K_d)(1-T)\frac{D}{E}Ke=Ku+(Ku−Kd)(1−T)ED
Substitute:
14=Ku+(Ku−6)×0.8×0.2514 = K_u + (K_u - 6)\times 0.8 \times 0.2514=Ku+(Ku−6)×0.8×0.25 14=Ku+0.2(Ku−6)14 = K_u + 0.2(K_u - 6)14=Ku+0.2(Ku−6) 14=1.2Ku−1.214 = 1.2K_u - 1.214=1.2Ku−1.2 1.2Ku=15.2⇒Ku≈12.67%1.2K_u = 15.2 \Rightarrow K_u \approx 12.67\%1.2Ku=15.2⇒Ku≈12.67%
Step 3 – Re-gear the cost of equity for the new structure
New target mix: Debt : Equity = 40 : 60 ⇒
DE=4060=0.6667\frac{D}{E} = \frac{40}{60} = 0.6667ED=6040=0.6667
Reapply MM with tax:
Ke′=Ku+(Ku−Kd)(1−T)DEK_e' = K_u + (K_u - K_d)(1-T)\frac{D}{E}Ke′=Ku+(Ku−Kd)(1−T)ED Ke′=12.67+(12.67−6)×0.8×0.6667K_e' = 12.67 + (12.67 - 6)\times 0.8 \times 0.6667Ke′=12.67+(12.67−6)×0.8×0.6667 Ke′≈12.67+3.56=16.23%K_e' \approx 12.67 + 3.56 = 16.23\%Ke′≈12.67+3.56=16.23%
Step 4 – Calculate new WACC
New proportions:
E/V=60100=0.6,D/V=40100=0.4E/V = \frac{60}{100} = 0.6,\quad D/V = \frac{40}{100} = 0.4E/V=10060=0.6,D/V=10040=0.4 WACC′=0.6×16.23%+0.4×4.8%\text{WACC}' = 0.6 \times 16.23\% + 0.4 \times 4.8\%WACC′=0.6×16.23%+0.4×4.8% WACC′≈9.74%+1.92%=11.66%\text{WACC}' \approx 9.74\% + 1.92\% = 11.66\%WACC′≈9.74%+1.92%=11.66%